Resolución de sudokus (18)

Pares remotos

Veamos otro patrón que nos puede permitir eliminar candidatos en algunas casillas.

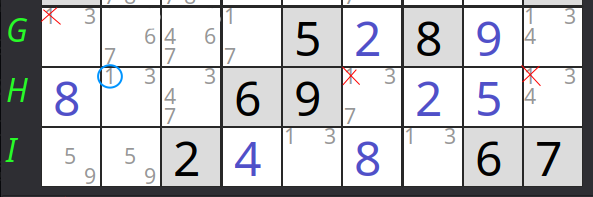
En la imagen de la derecha vemos dos casillas, en amarillo, con el mismo par de candidatos, 1 y 3. Estas casillas ocupan filas diferentes en cajas diferentes, en este ejemplo están en las filas H e I, ambas en la tercera fila de cajas, las cajas 7 y 9.

Además, si nos fijamos en la otra caja de esa fila de cajas, la 8, y en su fila restante, la G; las tres casillas que están marcadas en naranja, uno de los candidatos del par remoto no aparece como candidato o como valor final en ninguna de ellas. En este caso el 3 no aparece en G4, G5 ni G6, aunque sí el 1, que aparece como candidato en G4.

Este método nos dice que podemos eliminar el 1 como candidato en las casillas que comparten caja y fila con cada una de las casillas con el par de candidatos, es decir, en las casillas H7, H8, H9, I1, I2, e I3. En este caso sólo podemos eliminar el candidato 1 en la casilla H9 marcada en azul.

Por supuesto, el mismo patrón se puede aplicar a columnas de cajas.

Explicación

La lógica de este patrón es la siguiente:

• Para la casilla H2 tenemos dos situaciones posibles: o bien hay un 1 o bien un 3.
• Si el valor de la casilla H2 es 1, eso eliminaría el 1 como candidato en el resto de la caja 7 y de la fila H.



• Si el valor de la casilla H2 es 3, en la caja 8 podemos eliminar como candidato el 3 en la fila H, y sabemos (por la definición del patrón), que el 3 no es un candidato en la fila G de la caja 8. Por lo tanto, el 3 sólo puede estar en la fila I de esla caja. Esto a us vez implica que en I7 el 3 no es un candidato, y deberá ser un 1. Y finalemnte, eso elimina el 1 como candidato en el resto de la caja 9 y de la fila H.

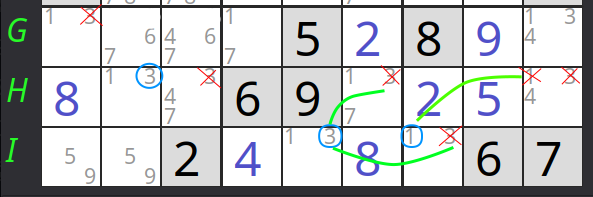
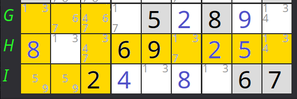
Esto define dos zonas en las que no puede haber un 1 como candidato: la caja 7 y fila H, menos H2, y la caja 9 y fila I, menos I7.

Ambas zonas tienen en común seis casillas: H7, H8, H9, I1, I2, e I3 .

Por lo tanto, podemos eliminar el candidato 1 de esas casillas en las que esté presente.

Patrón con eliminación de dos valores

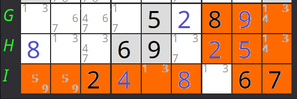
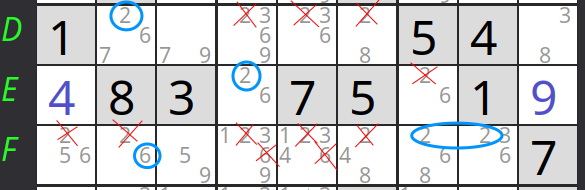
Puede suceder que en la tercera caja, la que no ocupa ninguna de las casillas con el par de candidatos, no aparezca ninguno de esos candidatos, como ocurre con el ejemplo de la izquierda. Ni el 2, ni el 6 aparecen como candidatos o valores finales en D7, D8 o D9, marcadas en naranja.

En ese caso podemos eliminar los dos candidatos en las casillas que comparten zona, en este ejemplo, E1, E2, E3, F4, F5 y F6.

La explicación es similar:

• Tomemos, por ejemplo, la casilla E4, que tiene dos posibilidades, contendrá o bien un 2, o bien un 6.
• Si en E4 hay un 2, podemos eliminar como candidato el 2 en la caja 5 y en la fila E.
• Por otra parte, sabemos que en la caja 6 el 2 no aparece como candidato en la fila D, y como está en E4, tampoco en la E. Por lo tanto ha de estar en la fila F, es decir, en F7, F8 o F9. Esto elimina como candidato el 2 en el resto de la fila F de la caja 4. Por lo tanto en F2 ha de haber un 6, lo que elimina como candidato el 6 en el resto de la caja.
• En resumen, si E4 contiene un 2, el 2 no puede ser candidato en la fila E y en la caja 5, salvo en E4, y el 6 no puede ser candidato en la fila F y en la caja 4, salvo en F2.



• Si por el contrario, en H4 hay un 6, podemos eliminar el 6 en la caja 5 y en la fila E.
• Y aplicando el mismo razonamiento que antes, en la caja 6, el 6 sólo puede estar en la fila F, ya que sabemos que en la fila D de la caja 6 es 6 no es un candidato.
• Eso elimina como candidato el 6 en la fila F de la caja 4, por lo que F2 debe contener un 2.
• Resumiendo, si E4 contiene un 6, el 6 no puede ser candidato en la fila E y en la caja 5, salvo en E4, y el 2 no puede ser candidato en la fila F y en la caja 4, salvo en F2.



• Si superponemos las casillas prohibidas para el 2 en ambos casos, podemos eliminar el dos en las casillas: E1, E2, E3, F4, F5 y F6.
• Y sucede exactamente lo mismo para el 6.
• El resultado es que podemos eliminar como candidatos el 2 y el 6 en esas casillas. Para este ejemplo eliminaremos el 2 en F4, F5 y F6, y el 6 en F4 y F5.

Algoritmo

A la hora de implementar este método, seguiremos el siguiente algoritmo:

- Empezaremos a buscar en cada fila de cajas dos casillas con el mismo par de candidatos, v1 y v2. en cajas y filas diferentes: 
        Caja 1 con cajas 2 y 3, y caja 2 con caja 3. 
        Caja 4 con cajas 5 y 6, y caja 5 con 6. 
        Caja 7 con cajas 8 y 9, y caja 8 con 9.
- Si encontramos esas dos casillas, en las filas f1 y f2, de las cajas k1 y k2, verificamos si en las tres casillas de la fila f3, 
        distinta de f1 y f2 y la caja k3, distinta de k1 y k2, falta alguno de los candidatos, v1 o v2.
- Si es así, tenemos un posible patrón, sólo falta por verificar si es posible eliminar el candidato 
        presente en f3 de k3 de f1 de k2 y/o f2 de k1.
- O, en el caso de que en f3 de k3 no aparezca ninguno de los candidatos, eliminarlos de las filas f1 de k2 y f2 de k1.

Podemos repetir el proceso con las columnas de cajas.

Debido a que se trata de un patrón que probablemente sea más fácil de detectar que otros, lo buscaremos antes que el hilo de cometa, el pez espada y otros.

bool Tablero::ParRemotoFilas() {
    for(int fk=0; fk<3; fk++) { // Para cada fila de cajas
        if(BuscaParFilas(fk*3, fk*3+1, fk*3+2)) return true;
        if(BuscaParFilas(fk*3, fk*3+2, fk*3+1)) return true;
        if(BuscaParFilas(fk*3+1, fk*3+2, fk*3)) return true;
    }
    return false;
}

bool Tablero::BuscaParFilas(int k1, int k2, int k3) {
    Pareja par;
    int p1, p2, p3;
    int f1, f2, f3;
    int v1, v2;
    bool contienev1;
    bool contienev2;

    for(p1=0; p1<9; p1++) {
        if(caja[k1].Cas(p1)->Lapiz().CuentaMarcas() == 2) {
            for(p2=0; p2<9; p2++) {
                if(caja[k2].Cas(p2)->Fila() != caja[k1].Cas(p1)->Fila() &&
                   caja[k2].Cas(p2)->Lapiz() == caja[k1].Cas(p1)->Lapiz()) {
                    f1 = p1/3;
                    f2 = p2/3;
                    f3 = 3-f1-f2; // 3-0-1 = 2, 3-0-2=1, 3-1-2=0 se cumple
                    v1 = caja[k1].Cas(p1)->Lapiz().ValorMarca(1);
                    v2 = caja[k1].Cas(p1)->Lapiz().ValorMarca(2);
                    // Tenemos un par de casillas candidatas
                    // Verificar la fila que completa el patrón en f3 de k3
                    contienev1=contienev2=false;
                    for(p3=0; p3<3; p3++) {
                        contienev1 |= caja[k3].Cas(f3*3+p3)->Lapiz().ContieneMarca(v1) || caja[k3].Cas(f3*3+p3)->Valor()==v1;
                        contienev2 |= caja[k3].Cas(f3*3+p3)->Lapiz().ContieneMarca(v2) || caja[k3].Cas(f3*3+p3)->Valor()==v2;
                    }
                    par.Asigna(0, caja[k1].Cas(p1));
                    par.Asigna(1, caja[k2].Cas(p2));
                    if(!contienev1 && !contienev2 && ProcesarRemotoFila(par, k1, k2, k3, f1, f2, f3, v1, v2)) return true;
                    if(contienev1 && !contienev2 && ProcesarRemotoFila(par, k1, k2, k3, f1, f2, f3, v1)) return true;
                    if(contienev2 && !contienev1 && ProcesarRemotoFila(par, k1, k2, k3, f1, f2, f3, v2)) return true;
                }
            }
        }
    }
    return false;
}

Nota: a partir de ahora los programas de ejemplo basados en wxWidgets no incluirán el fichero de proyecto Code::Blocks, ya que esos ficheros incluyen referencias a librerías que cambian para cada versión de wxWidgets y para cada plataforma.
Para compilar los programas será necesario crear un nuevo proyecto vacío en el IDE que prefieras y añadir los ficheros incluidos en el zip.
Es posible que haya que añadir algunas rutas para que el compilador localice los ficheros de cabecera. En el caso de Code::Blocks hay que editar las opciones de proyecto y añadir la ruta "include" a la opción de "Search directories" del "compiler".